###########################################################
Bagging and Boosting
The bootstrap approach does the next best thing by taking repeated a random sample, with replacement, of the same size as the original sample.
Bagging: use the bootstrap approach which does the next best thing by taking repeated samples from the training data. We therefore end up with B different training data sets. We can train our method on each data set and then average all the predictions it will reduce the variance by sqrt(B).
Classification bagging then, for any particular X, there are two possible approaches: 1) Record the class that each bootstrapped data set predicts and provide an overall prediction to the most commonly occurring one.(Voting). 2) If our classifier produces probability estimates we can just average the probabilities and then predict to the class with the highest probability. (Vote approach and averaging the probability estimates.)
library(ipred)
bagging.fit <- bagging(Salary~., data = hitters.noNA, subset = tr, nbagg = 1000)
bagging.pred <- predict(bagging.fit, hitters.noNA, nbagg = 1000)[-tr]
mean((hitters.noNA$Salary[-tr] - bagging.pred)^2);
###########################################################
Boosting works in a similar way except that, in each iteration, in the algorithm (i.e. each new data set) it places more weight in the fitting procedure on observations that were misclassified in the previous iterations.
The algorithm:
Boosting allows one to produce a more flexible decision boundary than Bagging. The training error rate will go to zero, if we keep doing the boosting. Even the training error touch zero, the test error still will go down. (the plot)
Relative Influence Plots: The particular variable is chosen which gives maximum reduction in the RSS over simply fitting a constant over the whole region. call this quality i. the relative influence of Xi us sum of all these i over all region for which it provide the best split over all region. In boosting, we just sum up all the RI in different trees.
Partial plot: the relationship between one or more predictors after accounting for or averaging out the effects of all the other predictors.
function:
Boosting is often suffered from the overfitting, we also use the shrinkage as before to penalty and get much better prediction on test data.
library(gbm);
shrinkage.seq = seq(0, 0.5, length = 20);
boost.fit <- boost(Salary~., data = hitters.noNA, shrinkage = shrinkage.seq, subset = tr, n.trees = 1000, trace = F, distribution = "gaussian")
par(mfrow=c(2,2));
plot(boost.fit$shrinkage, boost.fit$error, type = 'b');
# Produce 2 partial dependence plots for the 2 most influential variables. Also produce a joint partial influence plot for these 2 variables
par(mfrow=c(1, 3));
plot(boost.fit, i = "CHmRun");
plot(boost.fit, i = "Walks");
plot(boost.fit, i = c("CHmRun", "Walks"));
###########################################################
SVM: basic idea of a support vector is to find the straight line that gives the biggest separation between the classes i.e. the points are as far from the line as possible. C is the minimum perpendicular distance between each point and the separating line. We find the line which maximizes C. This line is called the “optimal separating hyperplane”
in practice it is not usually possible to find a hyper-plane that perfectly separates two classes. In this situation we try to find the plane that gives the best separation between the points that are correctly classified subject to the points on the wrong side of the line not being off by too much. Let ξ*i represent the amount that the ith point is on the wrong side of the margin (the dashed line).we want to maximize C subject to restriction: ( <= constant).The constant is a tuning parameter that we choose.
basic idea of a support vector classifier Instead we can create transformations (or a basis) b1(x), b2(x), …, bM(x) and find the optimal hyper-plane in the space spanned by b1(X), b2(X), …, bM(X). we choose something called a Kernel function which takes the place of the basis. Common kernel functions include: Linear, Polynomial, Radial Basis, Sigmoid
library(e1071)
svmfit <- svm(Salary~., SalaryData, subset = tr);
svmpred <- predict(svmfit, SalaryData)[-tr];
table1 <- table(svmpred, SalaryData$Salary[-tr]);
table1
(table1[1, 1] + table1[2, 2])/sum(table1);
(table1[1, 2] + table1[2, 1])/sum(table1);
mean(svmpred != SalaryData$Salary[-tr])
svmfit <- svm(Salary~., SalaryData, subset = tr, kernel = "linear", cost = opti.cost);
svmfit <- svm(Salary~., SalaryData, subset = tr, kernel = "polynomial", cost = opti.cost);
svmfit <- svm(Salary~., SalaryData, subset = tr, kernel = "radial", cost = opti.cost);
svmfit <- svm(Salary~., SalaryData, subset = tr, kernel = "sigmoid", cost = opti.cost);
Sunday, October 26, 2008
Tuesday, October 21, 2008
Notes for nnet, tree
# use {nnet} to Neural Networks
Neural Networks were first developed as a model for the human brain: Getting a prediction for Y involves 2 steps.
First we get predictions for Z1,….,ZM (hidden units) using the X’s. Second we predict Y using Z1,….,ZM.
Regression Equation:
the simple example:
One common approach is to find the α’s and β’s that minimize RSS
Classification Equation
algorithm:
Given the Z’s and f(X)’s one can compute derivatives for the change in RSS as the α’s and β’s change. Hence we can either increase or decrease each α and β (according to the sign on the derivative) so as to reduce RSS.
By making M large enough, neural networks allow one to fit almost arbitrarily flexible. another example of a neural network fit where the test error rate starts to increase as we increase the number of hidden units.
This penalty (called weight decay) forces the neural network fit to be smoother. The penalty function: once we use weight decay in the fit the error rate becomes fairly insensitive to the number of hidden units (as long as we have enough).
dim(spam)
tr = 1:2500;
library(nnet)
# The nnet() function implements a single hidden layer neural network. The
# syntax is almost identical to that for lm() etc.
# There are five possible additional variables to feed nnet(). First we must tell
# it how many hidden units to use through the command size=?. We can also specify a
# decay value by decay=? (by default this is zero if we don’t specify anything).
# By default the maximum number of iterations it
# does is 100. You can change the default using maxit=?. Finally, if you
# are using nnet for a regression (rather than a classification) problem
# you need to set linout=T to tell nnet to use a linear output (rather
# than a sigmoid output that is used for a classification situation).
# Fit a neural network to your training data using 2 hidden units and 0 decay.
# decay parameter for weight decay. Default 0. It is the penalty on large coefficient
nnfit = nnet(email ~ ., spam, size = 2, subset = tr);
summary(nnfit)
# Refit the neural network with 10 hidden units and 0 decay.
nnfit = nnet(email ~ ., spam, size = 10, subset = tr);
# Use the nnet.cv() function (on the training data) to estimate the optimal decay for your data when using 10 hidden units.
decayseq <- 10^seq(-3, 0, length = 10)
nnfit <- nnet.cv(email ~ ., data = spam, size = 10, trace = T, decay = decayseq, cv = 5);
windows()
plot(nnfit$decay, nnfit$cv, type = "l", ylim = c(0.03, 0.08))
lines(nnfit$decay, nnfit$train, col = "red");
## use the optimal decay
nnfit=nnet(email~.,spam,subset=tr,size=10,decay=1.4678)
nnpred <- predict(nnfit, spam, type = "class");
table1 <- table(nnpred[-tr], spam[-tr, "email"])
table1;
(table1[1, 1] + table1[2, 2]) / sum(table1)
mean(nnpred[-tr] == spam[-tr, "email"])
mean(nnpred[-tr] != spam[-tr, "email"])
#######################################################################
## library(tree)
Tree: make predictions in a regression problem is to divide the predictor space (i.e. all the possible values for X1,X2,…,Xp) into distinct regions, say R1, R2,…,Rk. every X that falls in a particular region (say Rj) we make the same prediction create the partitions by iteratively splitting one of the X variables into two regions. We can always represent them using a tree structure. This provides a very simple way to explain the model to a non-expert
For region Rj the best prediction is simply the average of all the responses from our training data that fell in Rj.
We consider splitting into two regions, Xj larger than s and Xj less than s for all possible values of s and j. We then choose the s and j that results in the lowest RSS on the training data.
The end points of the tree are called “terminal nodes”.
Classification tree: For each region (or node) we predict the most common category among the training data within that region. but minimizing RSS no longer makes sense. We use the criteria minimize the gini index or cross-entropy. If the node has similar prob for each category, the entroy will be larger.
We can improve accuracy by “pruning” the tree; cutting off some of the terminal nodes. use cross validation to see which tree has the lowest error rate.
#######################################################################
library(tree)
tr=1:400;
OJ.tree <- tree(Purchase ~., OJdata, subset = tr);
summary(OJ.tree)
OJ.tree
plot(OJ.tree)
text(OJ.tree , pretty = 0, cex = 0.8)

tree.pred <- predict(OJ.tree, OJdata, type = "class")
table1 <- table(tree.pred[-tr], OJdata$Purchase[-tr])
table1
(table1[1, 1] + table1[2, 2])/sum(table1)
(table1[1, 2] + table1[2, 1])/sum(table1)
### Pruning the Tree #####################
## Use the cv.tree() function on the tree from question 1 to compute the cross validation statistics for different tree sizes.
# By default K=10 (i.e. the data is divided into 10 parts).
cv.OJ.tree <- cv.tree(OJ.tree, K = 30)
names(cv.OJ.tree);
windows()
par(mfrow = c(1, 2))
plot(cv.OJ.tree$size, cv.OJ.tree$dev, type ='b')
plot(cv.OJ.tree$k, cv.OJ.tree$dev, type ='b')
cv.OJ.tree$k[order(cv.OJ.tree$dev)[1]]
# k: cost-complexity parameter defining either a specific subtree of tree
# The k from the optimal cross validation is around 12.2.
prune.OJ.tree <- prune.tree(OJ.tree, k =12.3)
windows();
plot(prune.OJ.tree)
text(prune.OJ.tree , pretty = 0, cex = 0.8)
summary(prune.OJ.tree)
tree.pred <- predict(prune.OJ.tree, OJdata, type = "class")
table1 <- table(tree.pred[-tr], OJdata$Purchase[-tr])
table1
(table1[1, 1] + table1[2, 2])/sum(table1)
(table1[1, 2] + table1[2, 1])/sum(table1)
# The mindev part of this line controls how far the tree is grown
# (the default value is 0.01). As we choose larger values for mindev
# the tree is made smaller and as we make mindev larger we get bigger trees.
# Find the best dev
mindev.seq = 10^seq(-3, -1,length=100)
library(tree)
tr=1:800;
test.error <- c();
tree.size <- c();
for(j in 1:100){
OJ.tree <- tree(Purchase ~., OJdata, subset = tr, control = tree.control(nobs=800, mindev=mindev.seq[j]));
tmp1 <- summary(OJ.tree)$size
tree.size <- c(tree.size, tmp1);
tree.pred <- predict(OJ.tree, OJdata, type = "class")
table1 <- table(tree.pred[-tr], OJdata$Purchase[-tr])
tmp2 <- (table1[1, 2] + table1[2, 1])/sum(table1)
test.error <- c(test.error, tmp2);
}
Neural Networks were first developed as a model for the human brain: Getting a prediction for Y involves 2 steps.
First we get predictions for Z1,….,ZM (hidden units) using the X’s. Second we predict Y using Z1,….,ZM.
Regression Equation:
the simple example:
One common approach is to find the α’s and β’s that minimize RSS
Classification Equation
algorithm:
Given the Z’s and f(X)’s one can compute derivatives for the change in RSS as the α’s and β’s change. Hence we can either increase or decrease each α and β (according to the sign on the derivative) so as to reduce RSS.
By making M large enough, neural networks allow one to fit almost arbitrarily flexible. another example of a neural network fit where the test error rate starts to increase as we increase the number of hidden units.
This penalty (called weight decay) forces the neural network fit to be smoother. The penalty function: once we use weight decay in the fit the error rate becomes fairly insensitive to the number of hidden units (as long as we have enough).
dim(spam)
tr = 1:2500;
library(nnet)
# The nnet() function implements a single hidden layer neural network. The
# syntax is almost identical to that for lm() etc.
# There are five possible additional variables to feed nnet(). First we must tell
# it how many hidden units to use through the command size=?. We can also specify a
# decay value by decay=? (by default this is zero if we don’t specify anything).
# By default the maximum number of iterations it
# does is 100. You can change the default using maxit=?. Finally, if you
# are using nnet for a regression (rather than a classification) problem
# you need to set linout=T to tell nnet to use a linear output (rather
# than a sigmoid output that is used for a classification situation).
# Fit a neural network to your training data using 2 hidden units and 0 decay.
# decay parameter for weight decay. Default 0. It is the penalty on large coefficient
nnfit = nnet(email ~ ., spam, size = 2, subset = tr);
summary(nnfit)
# Refit the neural network with 10 hidden units and 0 decay.
nnfit = nnet(email ~ ., spam, size = 10, subset = tr);
# Use the nnet.cv() function (on the training data) to estimate the optimal decay for your data when using 10 hidden units.
decayseq <- 10^seq(-3, 0, length = 10)
nnfit <- nnet.cv(email ~ ., data = spam, size = 10, trace = T, decay = decayseq, cv = 5);
windows()
plot(nnfit$decay, nnfit$cv, type = "l", ylim = c(0.03, 0.08))
lines(nnfit$decay, nnfit$train, col = "red");
## use the optimal decay
nnfit=nnet(email~.,spam,subset=tr,size=10,decay=1.4678)
nnpred <- predict(nnfit, spam, type = "class");
table1 <- table(nnpred[-tr], spam[-tr, "email"])
table1;
(table1[1, 1] + table1[2, 2]) / sum(table1)
mean(nnpred[-tr] == spam[-tr, "email"])
mean(nnpred[-tr] != spam[-tr, "email"])
#######################################################################
## library(tree)
Tree: make predictions in a regression problem is to divide the predictor space (i.e. all the possible values for X1,X2,…,Xp) into distinct regions, say R1, R2,…,Rk. every X that falls in a particular region (say Rj) we make the same prediction create the partitions by iteratively splitting one of the X variables into two regions. We can always represent them using a tree structure. This provides a very simple way to explain the model to a non-expert
For region Rj the best prediction is simply the average of all the responses from our training data that fell in Rj.
We consider splitting into two regions, Xj larger than s and Xj less than s for all possible values of s and j. We then choose the s and j that results in the lowest RSS on the training data.
The end points of the tree are called “terminal nodes”.
Classification tree: For each region (or node) we predict the most common category among the training data within that region. but minimizing RSS no longer makes sense. We use the criteria minimize the gini index or cross-entropy. If the node has similar prob for each category, the entroy will be larger.
We can improve accuracy by “pruning” the tree; cutting off some of the terminal nodes. use cross validation to see which tree has the lowest error rate.
#######################################################################
library(tree)
tr=1:400;
OJ.tree <- tree(Purchase ~., OJdata, subset = tr);
summary(OJ.tree)
OJ.tree
plot(OJ.tree)
text(OJ.tree , pretty = 0, cex = 0.8)

tree.pred <- predict(OJ.tree, OJdata, type = "class")
table1 <- table(tree.pred[-tr], OJdata$Purchase[-tr])
table1
(table1[1, 1] + table1[2, 2])/sum(table1)
(table1[1, 2] + table1[2, 1])/sum(table1)
### Pruning the Tree #####################
## Use the cv.tree() function on the tree from question 1 to compute the cross validation statistics for different tree sizes.
# By default K=10 (i.e. the data is divided into 10 parts).
cv.OJ.tree <- cv.tree(OJ.tree, K = 30)
names(cv.OJ.tree);
windows()
par(mfrow = c(1, 2))
plot(cv.OJ.tree$size, cv.OJ.tree$dev, type ='b')
plot(cv.OJ.tree$k, cv.OJ.tree$dev, type ='b')
cv.OJ.tree$k[order(cv.OJ.tree$dev)[1]]
# k: cost-complexity parameter defining either a specific subtree of tree
# The k from the optimal cross validation is around 12.2.
prune.OJ.tree <- prune.tree(OJ.tree, k =12.3)
windows();
plot(prune.OJ.tree)
text(prune.OJ.tree , pretty = 0, cex = 0.8)
summary(prune.OJ.tree)
tree.pred <- predict(prune.OJ.tree, OJdata, type = "class")
table1 <- table(tree.pred[-tr], OJdata$Purchase[-tr])
table1
(table1[1, 1] + table1[2, 2])/sum(table1)
(table1[1, 2] + table1[2, 1])/sum(table1)
# The mindev part of this line controls how far the tree is grown
# (the default value is 0.01). As we choose larger values for mindev
# the tree is made smaller and as we make mindev larger we get bigger trees.
# Find the best dev
mindev.seq = 10^seq(-3, -1,length=100)
library(tree)
tr=1:800;
test.error <- c();
tree.size <- c();
for(j in 1:100){
OJ.tree <- tree(Purchase ~., OJdata, subset = tr, control = tree.control(nobs=800, mindev=mindev.seq[j]));
tmp1 <- summary(OJ.tree)$size
tree.size <- c(tree.size, tmp1);
tree.pred <- predict(OJ.tree, OJdata, type = "class")
table1 <- table(tree.pred[-tr], OJdata$Purchase[-tr])
tmp2 <- (table1[1, 2] + table1[2, 1])/sum(table1)
test.error <- c(test.error, tmp2);
}
notes for Polynomial Regression, Splines and GAM
Linear models have significant advantages in terms of interpretation/inference. However, standard linear regression has significant limitations in terms of prediction power. Polynomial Regression is just a particular kind of “Basis Function”.
# use MASS library
# Use the poly() function to fit a polynomial regression
library(MASS)
attach(Boston);
names(Boston)
polyfit2 <- lm(nox ~ poly(dis, 2));
summary(polyfit2)
polyfit3 <- lm(nox ~ poly(dis, 3));
summary(polyfit3)
# The plot of regression fit with power of 3:
windows();
plot(dis, nox);
lines(sort(dis), polyfit3$fit[order(dis)], col = 2, lwd = 3)
###########################################################
Instead of fitting a high dimensional polynomial over the entire range of x. a spline works by fitting different low dimensional polynomials over different regions of x. For example a cubic spline works by fitting a cubic y=ax3+bx2+cx+d but the coefficients a, b, c and d may differ depending on which part of x we are looking at. The more knots that are used the more flexible the spline is.
It appears from this example that there are 8 parameters (or degrees of freedom) for us to choose. However, in reality there are a number of constraints. For example it makes sense to insist that the cubic curves meet at the knots. To make the curve smooth we also insist that the first and second derivatives are equal at the knots. This means there are really only 5 parameters we get to choose. In general there will be 4 + #knots free parameters to choose between.
# Use the bs() function to fit a spline regression to nox (Y) and dis (X).
# require the {gam} and {splines} package
#############################################################
library(gam)
# Generate the B-spline basis matrix for a polynomial spline using bs(), basis function
# df: degrees of freedom; df = length(knots) + 3 + intercept = #knots + 4, since we make equal at knot points, first and second derivatives
# knots the internal breakpoints that define the spline. The default is NULL,
# which results in a basis for ordinary polynomial regression.
# degree: degree of the piecewise polynomial—default is 3 for cubic splines.
splinefit3 <- lm(nox ~ bs(dis, 3))
summary(splinefit3);
# df = 4, which means 1 knot
splinefit4 <- lm(nox ~ bs(dis, 4))
summary(splinefit4);
windows();
plot(dis, nox);
lines(sort(dis), splinefit4$fit[order(dis)], col = 2, lwd = 3)

# smoothspline
Smooth Spline: What we really want to do is find some function, say g(xi) such that it fits the observed data wells. However, if we don’t put any constraints on g(xi) then we can always set RSS equal to zero simply by choosing a g(xi) that interpolates all the Y’s. What we really want is a g that makes RSS small but is also smooth. A penalty on the integrative of second derivative of g(xi).
# cv ordinary (TRUE) or “generalized” cross-validation (GCV) when FALSE.
smoothfit <- smooth.spline(dis, nox, cv = T)
###########################################################
## Generalized additive model (GAM)
When we have several predictors and want to achieve a non-linear fit, a natural way to extend the multiple linear regression model is to replace each linear part, ßjXij, with fj(Xij) where fj is some smooth non-linear function.
Pros of GAM: (Generalized additive model)
1. By allowing one to fit a non-linear fj to each Xj, model non-linear relationships. 2. We can potentially make more accurate predictions.
3. Because we are fitting an additive model we can still examine the effect of each Xj on Y individually, still good for inference.
cons: The model is restricted to be additive. a simple interaction between X1 and X2 can’t automatically be modeled using GAM
We can extend logistic regression to allow for non-linear relationships using the GAM framework
###########################################################
gamfit = gam(nox ~ ., data = Boston); #same as lm, all linear functions
summary(gamfit)
par(mfrow=c(4, 4)); plot(gamfit);
# GAM to use non-linear fits for most of the variables.
# To do this we use the notation s(X) instead of X.
gamfit=gam(medv~s(crim)+s(zn)+s(indus)+chas+s(nox)+s(rm)+s(dis)+s(rad)+s(tax)+s(ptratio)+s(black)+s(lstat),data=Boston)
par(mfrow=c(4, 4)); plot(gamfit,se=T)

# Now use the significant non linear varialbes. and test the prediction power
tr=1:400
gamfit=gam(medv~crim+zn+indus+chas+nox+s(rm)+dis+rad+tax + ptratio+black+s(lstat),data=Boston,subset=tr) #s(x, df=4, spar=1)
mean((predict(gamfit,Boston)[-tr]-medv[-tr])^2)
# use MASS library
# Use the poly() function to fit a polynomial regression
library(MASS)
attach(Boston);
names(Boston)
polyfit2 <- lm(nox ~ poly(dis, 2));
summary(polyfit2)
polyfit3 <- lm(nox ~ poly(dis, 3));
summary(polyfit3)
# The plot of regression fit with power of 3:
windows();
plot(dis, nox);
lines(sort(dis), polyfit3$fit[order(dis)], col = 2, lwd = 3)
###########################################################
Instead of fitting a high dimensional polynomial over the entire range of x. a spline works by fitting different low dimensional polynomials over different regions of x. For example a cubic spline works by fitting a cubic y=ax3+bx2+cx+d but the coefficients a, b, c and d may differ depending on which part of x we are looking at. The more knots that are used the more flexible the spline is.
It appears from this example that there are 8 parameters (or degrees of freedom) for us to choose. However, in reality there are a number of constraints. For example it makes sense to insist that the cubic curves meet at the knots. To make the curve smooth we also insist that the first and second derivatives are equal at the knots. This means there are really only 5 parameters we get to choose. In general there will be 4 + #knots free parameters to choose between.
# Use the bs() function to fit a spline regression to nox (Y) and dis (X).
# require the {gam} and {splines} package
#############################################################
library(gam)
# Generate the B-spline basis matrix for a polynomial spline using bs(), basis function
# df: degrees of freedom; df = length(knots) + 3 + intercept = #knots + 4, since we make equal at knot points, first and second derivatives
# knots the internal breakpoints that define the spline. The default is NULL,
# which results in a basis for ordinary polynomial regression.
# degree: degree of the piecewise polynomial—default is 3 for cubic splines.
splinefit3 <- lm(nox ~ bs(dis, 3))
summary(splinefit3);
# df = 4, which means 1 knot
splinefit4 <- lm(nox ~ bs(dis, 4))
summary(splinefit4);
windows();
plot(dis, nox);
lines(sort(dis), splinefit4$fit[order(dis)], col = 2, lwd = 3)

# smoothspline
Smooth Spline: What we really want to do is find some function, say g(xi) such that it fits the observed data wells. However, if we don’t put any constraints on g(xi) then we can always set RSS equal to zero simply by choosing a g(xi) that interpolates all the Y’s. What we really want is a g that makes RSS small but is also smooth. A penalty on the integrative of second derivative of g(xi).
# cv ordinary (TRUE) or “generalized” cross-validation (GCV) when FALSE.
smoothfit <- smooth.spline(dis, nox, cv = T)
###########################################################
## Generalized additive model (GAM)
When we have several predictors and want to achieve a non-linear fit, a natural way to extend the multiple linear regression model is to replace each linear part, ßjXij, with fj(Xij) where fj is some smooth non-linear function.
Pros of GAM: (Generalized additive model)
1. By allowing one to fit a non-linear fj to each Xj, model non-linear relationships. 2. We can potentially make more accurate predictions.
3. Because we are fitting an additive model we can still examine the effect of each Xj on Y individually, still good for inference.
cons: The model is restricted to be additive. a simple interaction between X1 and X2 can’t automatically be modeled using GAM
We can extend logistic regression to allow for non-linear relationships using the GAM framework
###########################################################
gamfit = gam(nox ~ ., data = Boston); #same as lm, all linear functions
summary(gamfit)
par(mfrow=c(4, 4)); plot(gamfit);
# GAM to use non-linear fits for most of the variables.
# To do this we use the notation s(X) instead of X.
gamfit=gam(medv~s(crim)+s(zn)+s(indus)+chas+s(nox)+s(rm)+s(dis)+s(rad)+s(tax)+s(ptratio)+s(black)+s(lstat),data=Boston)
par(mfrow=c(4, 4)); plot(gamfit,se=T)

# Now use the significant non linear varialbes. and test the prediction power
tr=1:400
gamfit=gam(medv~crim+zn+indus+chas+nox+s(rm)+dis+rad+tax + ptratio+black+s(lstat),data=Boston,subset=tr) #s(x, df=4, spar=1)
mean((predict(gamfit,Boston)[-tr]-medv[-tr])^2)
note for best subset regression and ridge lasso regression
Best Subset Selection: run a linear regression for each possible combination of the X predictors. One simple approach would be to take the subset with the smallest RSS. Unfortunately, one can show that the model that includes all the variables will always have the smallest RSS. There are many measures that people use: Adjusted R2; AIC (Akaike information criterion); BIC (Bayesian information criterion); Cp (equivalent to AIC for linear regression)
What we would really like to do is to find the set of variables that give the lowest test (not training) error rate. If we have a large data set we can achieve this goal by splitting the data into training, and validation parts. We would then use the training part to build each possible model (i.e. the different combinations of variables) and choose the model that gave the lowest error rate when applied to the validation data. We can also split the data into training, validation and testing parts. We would then use the training part to build each possible model and choose the model that gave the lowest error rate when applied to the validation data. Finally, the error rate on the test data would give us an estimate of how well the method would work on new observations.
# lasso use {lars} package, ridge and optim.lm use {leaps} package
#######################################################################
# use leaps package to find the best linear model based on BIC AIC
# select 300 out of total 400 samples to be the training set and 100 be the test set.
###########################################################
# names(carseats)
# [1] "Sales" "CompPrice" "Income" "Advertising" "Population" "Price" "ShelveLoc" # "Age" "Education" "Urban" "US"
td=sample(400,300,replace=F);
carseat.train <- carseats[td, ]
carseat.test <- carseats[-td, ]
# use optim.lm function to try to select the “best” linear model from my training data:
###########################################################
"optim.lm" <-
function(data,y,val.size=NULL,cv=10,bic=T,test=T,really.big=F){
library(MASS)
library(leaps)
n.plots <- sum(c(bic,test,cv!=0))
par(mfrow=c(n.plots,1))
n <- nrow(data)
names(data)[(names(data)==y)] <- "y"
X <- lm(y~.,data,x=T)$x
data <- as.data.frame(cbind(data$y,X[,-1]))
names(data)[1] <- "y"
if (is.null(val.size))
val.size <- round(n/4)
s <- sample(n,val.size,replace=F)
data.train <- data[-s,]
data.test <- data[s,]
p <- ncol(data)-1
data.names <- names(data)[names(data)!="y"]
regfit.full <-
regsubsets(y~.,data=data,nvmax=p,nbest=1,really.big=really.big)
bic.lm <-
lm(as.formula(paste("y~",paste(data.names[summary(regfit.full)$which[order(summary(regfit.full)$bic)[1],][-1]],collapse="+"))),data=data)
if (bic){
plot(summary(regfit.full)$bic,type='l',xlab="Number of Predictors",
ylab="BIC",main="BIC Method")
points(summary(regfit.full)$bic,pch=20)
points(order(summary(regfit.full)$bic)[1],min(summary(regfit.full)$bic),col=2,pch=20,cex=1.5)}
regfit <- regsubsets(y~.,data=data.train,nvmax=p,nbest=1,really.big=really.big)
cv.rss <- rootmse <- rep(0,p)
for (i in 1:p){
data.lmfit <-lm(as.formula(paste("y~",paste(data.names[summary(regfit)$which[i,][-1]],collapse="+"))),data=data.train)
rootmse[i]<-sqrt(mean((predict(data.lmfit,data.test)-data.test$y)^2))}
if (test){
plot(rootmse,type='l',xlab="Number of Predictors",
ylab="Root Mean RSS on Validation Data",main="Validation Method")
points(rootmse,pch=20)
points(order(rootmse)[1],min(rootmse),col=2,pch=20,cex=1.5)}
validation.lm <-
lm(as.formula(paste("y~",paste(data.names[summary(regfit)$which[order(rootmse)[1],][-1]],collapse="+"))),data=data)
if (cv!=0){
s <- sample(cv,n,replace=T)
if (cv==n)
s <- 1:n
for (i in 1:p)
for (j in 1:cv){
data.train <- data[s!=j,]
data.test <- data[s==j,]
data.lmfit<-lm(as.formula(paste("y~",paste(data.names[summary(regfit.full)$which[i,][-1]],collapse="+"))),data=data.train)
cv.rss[i]<-cv.rss[i]+sum((predict(data.lmfit,data.test)-data.test$y)^2)
}
cv.rss <- sqrt(cv.rss/n)
plot(cv.rss,type='l',xlab="Number of Predictors",
ylab="Cross-Validated Root Mean RSS",main="Cross-Validation Method")
points(cv.rss,pch=20)
points(order(cv.rss)[1],min(cv.rss),col=2,pch=20,cex=1.5)
cv.lm <-
lm(as.formula(paste("y~",paste(data.names[summary(regfit.full)$which[order(cv.rss)[1],][-1]],collapse="+"))),data=data)}
else
cv.lm <- NULL
list(bic.lm = bic.lm,validation.lm=validation.lm,cv.lm=cv.lm)
}
library(leaps);
optim.lm.train <- optim.lm(carseat.train, "Sales");
names(optim.lm.train);
# Report the model selected by BIC, validation, or CV (cross validation)
summary(optim.lm.train$bic)
summary(optim.lm.train$validation)
summary(optim.lm.train$cv)
# Predict the residual sum of squares (or mean sum of squares) on my test data set.
# If we only use the mean of Y, the mean of sum squares is:
mean((carseats$Sales[-td] - mean(carseats$Sales[td]))^2)
# if we use model selected by BIC:
lm.bic=lm(Sales~CompPrice+Income+Advertising+Price+ShelveLoc+Age,data = carseats,subset=td);
# the mean of sum squares is:
mean((carseats$Sales[-td]-predict(lm.bic,carseats)[-td])^2);
#### ridge regression #####################################
Ridge Regression add a “penalty” on sum of squared betha. This has the effect of “shrinking” large values of beta towards zero. As a result the ridge regression estimates are often more accurate. Notice when lambda=0 we get OLS but as lambda gets larger the beta’s will get closer to zero: more shrinkage. Because: It turns out that the OLS estimates generally have low bias but can be highly variable. In particular when n and p are a similar size the OLS estimates will be extremely variable. The penalty term makes the ridge regression estimates biased but can also substantially reduce their variance.
# lambda is the penalty coefficient on the beta squares
# lambda 0, beta same as OLS
###########################################################
lambda.set <- 10^(seq(-2, 8, length = 100));
ridge.train <- lm.ridge(Sales~., carseats, subset = td, lambda = lambda.set)
select(ridge.train);
# modified HKB estimator is 0.6875941
# modified L-W estimator is 1.311013
# smallest value of GCV at 0.5214008
# The best lambda from GCV is 0.5214.
# Using this lambda, we can get the best model:
ridge.train.cv <- lm.ridge(Sales~., carseats, subset = td, lambda = 0.5214);
ridge.train.cv$coef;
ridge.pred.cv <- pred.ridge(ridge.train.cv, Sales~., carseats)
mean((carseats$Sales[-td] - ridge.pred.cv[-td])^2)
------ ## iterations ###############
rss.ridge <- rep(0, 100);
for(i in 1:100){
ridge.train <- lm.ridge(Sales~., carseats, subset = td, lambda = lambda.set[i]);
ridge.pred <- pred.ridge(ridge.train, Sales~., carseats);
rss.ridge[i] <- mean((carseats$Sales[-td] - ridge.pred[-td])^2);
}
min(rss.ridge);
plot(rss.ridge, type = "l")
best.lambda <- lambda.set[order(rss.ridge)[1]]
best.lambda;
ridge.best <- lm.ridge(Sales~., carseats, subset = td, lambda = best.lambda);
ridge.best$coef
#### LASSO #######################################################
Ridge Regression isn’t perfect. One significant problem is that the squared penalty will never force any of the coefficients to be exactly zero. Hence the final model will include all variables, making it harder to interpret. A very modern alternative is the LASSO. The LASSO works in a similar way to ridge regression except that it uses an L1 penalty. LASSO is not quite as computational efficient as ridge regression, however, there are efficient algorithm exist and still faster than subset selection.
# s is the constraint sum |beta| < s, s infinity, beta same as OLS
###################################################################
"cv.lasso" <-
function(formula,data,subset=NULL,K=10){
if (!is.null(subset))
data <- data[subset,]
y <- data[,names(data)==as.character(formula)[2]]
x <- model.matrix(as.formula(formula),data)[,-1]
larsfit <- cv.lars(x,y,K=K)
larsfit
}
"lasso" <-
function(formula,data,subset=NULL){
if (!is.null(subset))
data <- data[subset,]
y <- data[,names(data)==as.character(formula)[2]]
x <- model.matrix(as.formula(formula),data)[,-1]
larsfit <- lars(x,y,type="lasso")
larsfit
}
library(lars);
lasso.fit <- lasso(Sales~., carseats, subset = td);
plot(lasso.fit);
lasso.fit
## use cv.lasso to get best s:
lasso.cv <- cv.lasso(Sales~., carseats, subset = td);
s <- lasso.cv$fraction[order(lasso.cv$cv)[1]]
s
lasso.pred <- pred.lasso(lasso.fit, Sales~., carseats, s)
mean((carseats$Sales[-td] - lasso.pred[-td])^2);
pred.lasso(lasso.fit, Sales~., carseats, s, "coefficients")
#### iterations #########
s.set <- seq(0, 1, length = 100);
rss.lasso <- rep(0, 100);
for(i in 1:100){
lasso.pred <- pred.lasso(lasso.fit, Sales~., carseats, s = s.set[i]);
rss.lasso[i] <- mean((carseats$Sales[-td] - lasso.pred[-td])^2);
}
min(rss.lasso)
plot(rss.lasso,type="l")
s <- s.set[order(rss.lasso)[1]];
s
pred.lasso(lasso.fit, Sales~., carseats, s, "coefficients")
###########################################################
# we plot just predict mean, OLS, BIC, ridge regression and the
# LASSO in one plot, it can be explained more clearly.
rss.raw=mean((carseats$Sales[-td]-mean(carseats$Sales[td]))^2)
rss.raw
lmfit=lm(Sales~.,carseats,subset=td)
rss.ols=mean((carseats$Sales[-td]-predict(lmfit,carseats)[-td])^2)
rss.ols
plot(1:100,1:100,ylim=c(1,10),ylab="Test Mean RSS",xlab="Tuning Parameter", type="n")
abline(rss.raw,0,lwd=1,lty=2, col = "green")
abline(rss.ols,0,lwd=1,lty=3, col = "blue")
abline(rss.bic,0,lwd=1,lty=4, col = "grey")
lines(rss.lasso,lwd=1,lty=5, col = "red")
lines(rss.ridge,lwd=1,lty=6, col = "orange")
legend(70,7,c("Raw","OLS","BIC","LASSO","Ridge"),col = c("green", "blue", "grey", "red", "orange"), lty=c(2,3,4,5,1),lwd=1)
# OLS with all the variables give the smallest RSS,
# while the simple mean give the largest RSS

What we would really like to do is to find the set of variables that give the lowest test (not training) error rate. If we have a large data set we can achieve this goal by splitting the data into training, and validation parts. We would then use the training part to build each possible model (i.e. the different combinations of variables) and choose the model that gave the lowest error rate when applied to the validation data. We can also split the data into training, validation and testing parts. We would then use the training part to build each possible model and choose the model that gave the lowest error rate when applied to the validation data. Finally, the error rate on the test data would give us an estimate of how well the method would work on new observations.
# lasso use {lars} package, ridge and optim.lm use {leaps} package
#######################################################################
# use leaps package to find the best linear model based on BIC AIC
# select 300 out of total 400 samples to be the training set and 100 be the test set.
###########################################################
# names(carseats)
# [1] "Sales" "CompPrice" "Income" "Advertising" "Population" "Price" "ShelveLoc" # "Age" "Education" "Urban" "US"
td=sample(400,300,replace=F);
carseat.train <- carseats[td, ]
carseat.test <- carseats[-td, ]
# use optim.lm function to try to select the “best” linear model from my training data:
###########################################################
"optim.lm" <-
function(data,y,val.size=NULL,cv=10,bic=T,test=T,really.big=F){
library(MASS)
library(leaps)
n.plots <- sum(c(bic,test,cv!=0))
par(mfrow=c(n.plots,1))
n <- nrow(data)
names(data)[(names(data)==y)] <- "y"
X <- lm(y~.,data,x=T)$x
data <- as.data.frame(cbind(data$y,X[,-1]))
names(data)[1] <- "y"
if (is.null(val.size))
val.size <- round(n/4)
s <- sample(n,val.size,replace=F)
data.train <- data[-s,]
data.test <- data[s,]
p <- ncol(data)-1
data.names <- names(data)[names(data)!="y"]
regfit.full <-
regsubsets(y~.,data=data,nvmax=p,nbest=1,really.big=really.big)
bic.lm <-
lm(as.formula(paste("y~",paste(data.names[summary(regfit.full)$which[order(summary(regfit.full)$bic)[1],][-1]],collapse="+"))),data=data)
if (bic){
plot(summary(regfit.full)$bic,type='l',xlab="Number of Predictors",
ylab="BIC",main="BIC Method")
points(summary(regfit.full)$bic,pch=20)
points(order(summary(regfit.full)$bic)[1],min(summary(regfit.full)$bic),col=2,pch=20,cex=1.5)}
regfit <- regsubsets(y~.,data=data.train,nvmax=p,nbest=1,really.big=really.big)
cv.rss <- rootmse <- rep(0,p)
for (i in 1:p){
data.lmfit <-lm(as.formula(paste("y~",paste(data.names[summary(regfit)$which[i,][-1]],collapse="+"))),data=data.train)
rootmse[i]<-sqrt(mean((predict(data.lmfit,data.test)-data.test$y)^2))}
if (test){
plot(rootmse,type='l',xlab="Number of Predictors",
ylab="Root Mean RSS on Validation Data",main="Validation Method")
points(rootmse,pch=20)
points(order(rootmse)[1],min(rootmse),col=2,pch=20,cex=1.5)}
validation.lm <-
lm(as.formula(paste("y~",paste(data.names[summary(regfit)$which[order(rootmse)[1],][-1]],collapse="+"))),data=data)
if (cv!=0){
s <- sample(cv,n,replace=T)
if (cv==n)
s <- 1:n
for (i in 1:p)
for (j in 1:cv){
data.train <- data[s!=j,]
data.test <- data[s==j,]
data.lmfit<-lm(as.formula(paste("y~",paste(data.names[summary(regfit.full)$which[i,][-1]],collapse="+"))),data=data.train)
cv.rss[i]<-cv.rss[i]+sum((predict(data.lmfit,data.test)-data.test$y)^2)
}
cv.rss <- sqrt(cv.rss/n)
plot(cv.rss,type='l',xlab="Number of Predictors",
ylab="Cross-Validated Root Mean RSS",main="Cross-Validation Method")
points(cv.rss,pch=20)
points(order(cv.rss)[1],min(cv.rss),col=2,pch=20,cex=1.5)
cv.lm <-
lm(as.formula(paste("y~",paste(data.names[summary(regfit.full)$which[order(cv.rss)[1],][-1]],collapse="+"))),data=data)}
else
cv.lm <- NULL
list(bic.lm = bic.lm,validation.lm=validation.lm,cv.lm=cv.lm)
}
library(leaps);
optim.lm.train <- optim.lm(carseat.train, "Sales");
names(optim.lm.train);
# Report the model selected by BIC, validation, or CV (cross validation)
summary(optim.lm.train$bic)
summary(optim.lm.train$validation)
summary(optim.lm.train$cv)
# Predict the residual sum of squares (or mean sum of squares) on my test data set.
# If we only use the mean of Y, the mean of sum squares is:
mean((carseats$Sales[-td] - mean(carseats$Sales[td]))^2)
# if we use model selected by BIC:
lm.bic=lm(Sales~CompPrice+Income+Advertising+Price+ShelveLoc+Age,data = carseats,subset=td);
# the mean of sum squares is:
mean((carseats$Sales[-td]-predict(lm.bic,carseats)[-td])^2);
#### ridge regression #####################################
Ridge Regression add a “penalty” on sum of squared betha. This has the effect of “shrinking” large values of beta towards zero. As a result the ridge regression estimates are often more accurate. Notice when lambda=0 we get OLS but as lambda gets larger the beta’s will get closer to zero: more shrinkage. Because: It turns out that the OLS estimates generally have low bias but can be highly variable. In particular when n and p are a similar size the OLS estimates will be extremely variable. The penalty term makes the ridge regression estimates biased but can also substantially reduce their variance.
# lambda is the penalty coefficient on the beta squares
# lambda 0, beta same as OLS
###########################################################
lambda.set <- 10^(seq(-2, 8, length = 100));
ridge.train <- lm.ridge(Sales~., carseats, subset = td, lambda = lambda.set)
select(ridge.train);
# modified HKB estimator is 0.6875941
# modified L-W estimator is 1.311013
# smallest value of GCV at 0.5214008
# The best lambda from GCV is 0.5214.
# Using this lambda, we can get the best model:
ridge.train.cv <- lm.ridge(Sales~., carseats, subset = td, lambda = 0.5214);
ridge.train.cv$coef;
ridge.pred.cv <- pred.ridge(ridge.train.cv, Sales~., carseats)
mean((carseats$Sales[-td] - ridge.pred.cv[-td])^2)
------ ## iterations ###############
rss.ridge <- rep(0, 100);
for(i in 1:100){
ridge.train <- lm.ridge(Sales~., carseats, subset = td, lambda = lambda.set[i]);
ridge.pred <- pred.ridge(ridge.train, Sales~., carseats);
rss.ridge[i] <- mean((carseats$Sales[-td] - ridge.pred[-td])^2);
}
min(rss.ridge);
plot(rss.ridge, type = "l")
best.lambda <- lambda.set[order(rss.ridge)[1]]
best.lambda;
ridge.best <- lm.ridge(Sales~., carseats, subset = td, lambda = best.lambda);
ridge.best$coef
#### LASSO #######################################################
Ridge Regression isn’t perfect. One significant problem is that the squared penalty will never force any of the coefficients to be exactly zero. Hence the final model will include all variables, making it harder to interpret. A very modern alternative is the LASSO. The LASSO works in a similar way to ridge regression except that it uses an L1 penalty. LASSO is not quite as computational efficient as ridge regression, however, there are efficient algorithm exist and still faster than subset selection.
# s is the constraint sum |beta| < s, s infinity, beta same as OLS
###################################################################
"cv.lasso" <-
function(formula,data,subset=NULL,K=10){
if (!is.null(subset))
data <- data[subset,]
y <- data[,names(data)==as.character(formula)[2]]
x <- model.matrix(as.formula(formula),data)[,-1]
larsfit <- cv.lars(x,y,K=K)
larsfit
}
"lasso" <-
function(formula,data,subset=NULL){
if (!is.null(subset))
data <- data[subset,]
y <- data[,names(data)==as.character(formula)[2]]
x <- model.matrix(as.formula(formula),data)[,-1]
larsfit <- lars(x,y,type="lasso")
larsfit
}
library(lars);
lasso.fit <- lasso(Sales~., carseats, subset = td);
plot(lasso.fit);
lasso.fit
## use cv.lasso to get best s:
lasso.cv <- cv.lasso(Sales~., carseats, subset = td);
s <- lasso.cv$fraction[order(lasso.cv$cv)[1]]
s
lasso.pred <- pred.lasso(lasso.fit, Sales~., carseats, s)
mean((carseats$Sales[-td] - lasso.pred[-td])^2);
pred.lasso(lasso.fit, Sales~., carseats, s, "coefficients")
#### iterations #########
s.set <- seq(0, 1, length = 100);
rss.lasso <- rep(0, 100);
for(i in 1:100){
lasso.pred <- pred.lasso(lasso.fit, Sales~., carseats, s = s.set[i]);
rss.lasso[i] <- mean((carseats$Sales[-td] - lasso.pred[-td])^2);
}
min(rss.lasso)
plot(rss.lasso,type="l")
s <- s.set[order(rss.lasso)[1]];
s
pred.lasso(lasso.fit, Sales~., carseats, s, "coefficients")
###########################################################
# we plot just predict mean, OLS, BIC, ridge regression and the
# LASSO in one plot, it can be explained more clearly.
rss.raw=mean((carseats$Sales[-td]-mean(carseats$Sales[td]))^2)
rss.raw
lmfit=lm(Sales~.,carseats,subset=td)
rss.ols=mean((carseats$Sales[-td]-predict(lmfit,carseats)[-td])^2)
rss.ols
plot(1:100,1:100,ylim=c(1,10),ylab="Test Mean RSS",xlab="Tuning Parameter", type="n")
abline(rss.raw,0,lwd=1,lty=2, col = "green")
abline(rss.ols,0,lwd=1,lty=3, col = "blue")
abline(rss.bic,0,lwd=1,lty=4, col = "grey")
lines(rss.lasso,lwd=1,lty=5, col = "red")
lines(rss.ridge,lwd=1,lty=6, col = "orange")
legend(70,7,c("Raw","OLS","BIC","LASSO","Ridge"),col = c("green", "blue", "grey", "red", "orange"), lty=c(2,3,4,5,1),lwd=1)
# OLS with all the variables give the smallest RSS,
# while the simple mean give the largest RSS

note for linear and logistic regression
# general way of linear and logistic regression
One common measure of accuracy is the residual sum of squares , U shape means non-linear relationship, normal quantile plot for normality, constant variance of error terms, independence of error terms.
# simple regression
car[1:10, ];
library(MASS)
lm.simple1 <- lm(Mpg ~ Weight, data = car);
summary(lm.simple1);
###########################################################
windows(); # plot the fitted line
plot(car$Weight, car$Mpg, xlab = "Weight", ylab = "Mpg");
abline(lm.simple1, col = "red");
###########################################################
windows(); # resid ~ x plots see any dependency
plot(car$Weight, residuals(lm.simple1), xlab = "Weight", ylab = "resids");
abline(h = 0, col = "red");
lines(loess.smooth(car$Weight, residuals(lm.simple1)), col = "green", lty = 5);
###########################################################
windows(); # std error against the fitted value
plot(fitted(lm.simple1), stdres(lm.simple1), xlab = "Fitted Mpg", ylab = "standardized resids");
abline(h = 0, col = "red");
lines(loess.smooth(fitted(lm.simple1), stdres(lm.simple1)), col = "green", lty = 5);
###########################################################
windows(20 ,20)
par(mfrow=c(2,2))
plot(density(stdres(lm.simple1)), main = "density of standardized residuals")
qqnorm(stdres(lm.simple1)); # QQ plot of the std errors
qqline(stdres(lm.simple1))
###########################################################
# Multiple Linear Regression
###########################################################
pairs(car);
lm.mlti <- lm(Mpg ~ Cylind. + Disp. + Horse. + Weight + Accel. + Year + Origin, data = car)
# dot say use all the variable in data except Mpg to do linear regression
lm.mlti <- lm(Mpg ~ ., data = car)
summary(lm.mlti)
# .-Weight say use all the variable in data except Mpg and Weight to do linear regression
lm.mlti <- lm(Mpg ~ .-Weight, data = car)
# means Disp. + Weight + Disp.:Weight (interactions)
lm.mlti.e <- lm(Mpg ~ Disp. * Weight, data = car)
summary(lm.mlti.e)
###########################################################
## Logistic Regression, use glm function
###########################################################
glm.CYT <- glm(Loc_CYT ~ mcg + gvh + alm + mit + erl + pox + vac + nuc, family = binomial, data = dataset_new);
summary(glm.CYT);
contrasts(dataset_new$Loc_CYT);
table1 <- table(predict(glm.CYT1, type = "response") > 0.5, dataset_new$Loc_CYT); # confusion table
table1
size <- dim(dataset_new);
## check the prediction accuracy
(table1[1, 1] + table1[2, 2]) / size[1];
## use partial of the dataset as training dataset, the others as test dataset:
glm.CYT5 <- glm(Loc_CYT ~ gvh + alm + mit + nuc, family = binomial,
data = dataset_new, subset = 1:900);
table2 <- table(predict(glm.CYT5, dataset_new, type = "response")[-(1:900)] > 0.5,
dataset_new$Loc_CYT[-(1:900)]);
table2
(table2[1, 1] + table2[2, 2]) / (size[1] - 900);
####################################################
A good website can be find here:
http://www.statmethods.net/stats/regression.html
One common measure of accuracy is the residual sum of squares , U shape means non-linear relationship, normal quantile plot for normality, constant variance of error terms, independence of error terms.
# simple regression
car[1:10, ];
library(MASS)
lm.simple1 <- lm(Mpg ~ Weight, data = car);
summary(lm.simple1);
###########################################################
windows(); # plot the fitted line
plot(car$Weight, car$Mpg, xlab = "Weight", ylab = "Mpg");
abline(lm.simple1, col = "red");
###########################################################
windows(); # resid ~ x plots see any dependency
plot(car$Weight, residuals(lm.simple1), xlab = "Weight", ylab = "resids");
abline(h = 0, col = "red");
lines(loess.smooth(car$Weight, residuals(lm.simple1)), col = "green", lty = 5);
###########################################################
windows(); # std error against the fitted value
plot(fitted(lm.simple1), stdres(lm.simple1), xlab = "Fitted Mpg", ylab = "standardized resids");
abline(h = 0, col = "red");
lines(loess.smooth(fitted(lm.simple1), stdres(lm.simple1)), col = "green", lty = 5);
###########################################################
windows(20 ,20)
par(mfrow=c(2,2))
plot(density(stdres(lm.simple1)), main = "density of standardized residuals")
qqnorm(stdres(lm.simple1)); # QQ plot of the std errors
qqline(stdres(lm.simple1))
###########################################################
# Multiple Linear Regression
###########################################################
pairs(car);
lm.mlti <- lm(Mpg ~ Cylind. + Disp. + Horse. + Weight + Accel. + Year + Origin, data = car)
# dot say use all the variable in data except Mpg to do linear regression
lm.mlti <- lm(Mpg ~ ., data = car)
summary(lm.mlti)
# .-Weight say use all the variable in data except Mpg and Weight to do linear regression
lm.mlti <- lm(Mpg ~ .-Weight, data = car)
# means Disp. + Weight + Disp.:Weight (interactions)
lm.mlti.e <- lm(Mpg ~ Disp. * Weight, data = car)
summary(lm.mlti.e)
###########################################################
## Logistic Regression, use glm function
###########################################################
glm.CYT <- glm(Loc_CYT ~ mcg + gvh + alm + mit + erl + pox + vac + nuc, family = binomial, data = dataset_new);
summary(glm.CYT);
contrasts(dataset_new$Loc_CYT);
table1 <- table(predict(glm.CYT1, type = "response") > 0.5, dataset_new$Loc_CYT); # confusion table
table1
size <- dim(dataset_new);
## check the prediction accuracy
(table1[1, 1] + table1[2, 2]) / size[1];
## use partial of the dataset as training dataset, the others as test dataset:
glm.CYT5 <- glm(Loc_CYT ~ gvh + alm + mit + nuc, family = binomial,
data = dataset_new, subset = 1:900);
table2 <- table(predict(glm.CYT5, dataset_new, type = "response")[-(1:900)] > 0.5,
dataset_new$Loc_CYT[-(1:900)]);
table2
(table2[1, 1] + table2[2, 2]) / (size[1] - 900);
####################################################
A good website can be find here:
http://www.statmethods.net/stats/regression.html
display 3d plots
x=seq(-pi,pi,len=50)
y=x;
f=outer(x,y,function(x,y)cos(y)/(1+x^2));
f[1:5, 1:5]
# The contour() function produces a contour map and is used for three
# dimensional data (like mountains). You feed it three inputs. The first
# is a vector of the x values, the second a vector of the y values and
# the third is a matrix with each element corresponding to the Z value
# (the third dimension) for each pair of (x,y) coordinates. Just like
# plot there are many other things you can feed it to. See the help file.
contour(x,y,f)
contour(x,y,f,nlevels=15)
# persp() works the same as image() and contour() but it actually
# produces a 3d plot. theta an phi control the various angles you can look
# at the plot from.
persp(x,y,f)
persp(x,y,f,theta=30)
persp(x,y,f,theta=30,phi=20)

########################################################################
## another example of 3d plot from my personal reserach, use rgl library
########################################################################
# 3D visualization device system
library(rgl);
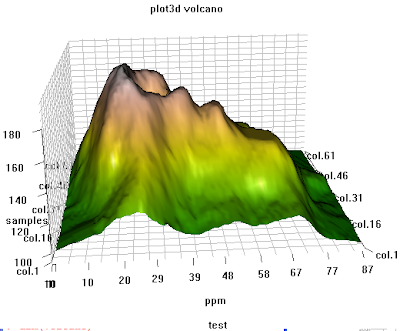
data(volcano)
dim(volcano)
peak.height <- volcano;
ppm.index <- (1:nrow(volcano));
sample.index <- (1:ncol(volcano));
zlim <- range(peak.height)
zlen <- zlim[2] - zlim[1] + 1
colorlut <- terrain.colors(zlen) # height color lookup table
col <- colorlut[(peak.height-zlim[1]+1)] # assign colors to heights for each point
open3d()
ppm.index1 <- ppm.index*zlim[2]/max(ppm.index);
sample.index1 <- sample.index*zlim[2]/max(sample.index)
title.name <- paste("plot3d ", "volcano", sep = "");
surface3d(ppm.index1, sample.index1, peak.height, color=col, back="lines", main = title.name);
grid3d(c("x", "y+", "z"), n =20)
sample.name <- paste("col.", 1:ncol(volcano), sep="");
sample.label <- as.integer(seq(1, length(sample.name), length = 5));
axis3d('y+',at = sample.index1[sample.label], sample.name[sample.label], cex = 0.3);
axis3d('y',at = sample.index1[sample.label], sample.name[sample.label], cex = 0.3)
axis3d('z',pos=c(0, 0, NA))
ppm.label <- as.integer(seq(1, length(ppm.index), length = 10));
axes3d('x', at=c(ppm.index1[ppm.label], 0, 0), abs(round(ppm.index[ppm.label], 2)), cex = 0.3);
title3d(main = title.name, sub = "test", xlab = "ppm", ylab = "samples", zlab = "peak")
rgl.bringtotop();
y=x;
f=outer(x,y,function(x,y)cos(y)/(1+x^2));
f[1:5, 1:5]
# The contour() function produces a contour map and is used for three
# dimensional data (like mountains). You feed it three inputs. The first
# is a vector of the x values, the second a vector of the y values and
# the third is a matrix with each element corresponding to the Z value
# (the third dimension) for each pair of (x,y) coordinates. Just like
# plot there are many other things you can feed it to. See the help file.
contour(x,y,f)
contour(x,y,f,nlevels=15)
# persp() works the same as image() and contour() but it actually
# produces a 3d plot. theta an phi control the various angles you can look
# at the plot from.
persp(x,y,f)
persp(x,y,f,theta=30)
persp(x,y,f,theta=30,phi=20)

########################################################################
## another example of 3d plot from my personal reserach, use rgl library
########################################################################
# 3D visualization device system
library(rgl);
data(volcano)
dim(volcano)
peak.height <- volcano;
ppm.index <- (1:nrow(volcano));
sample.index <- (1:ncol(volcano));
zlim <- range(peak.height)
zlen <- zlim[2] - zlim[1] + 1
colorlut <- terrain.colors(zlen) # height color lookup table
col <- colorlut[(peak.height-zlim[1]+1)] # assign colors to heights for each point
open3d()
ppm.index1 <- ppm.index*zlim[2]/max(ppm.index);
sample.index1 <- sample.index*zlim[2]/max(sample.index)
title.name <- paste("plot3d ", "volcano", sep = "");
surface3d(ppm.index1, sample.index1, peak.height, color=col, back="lines", main = title.name);
grid3d(c("x", "y+", "z"), n =20)
sample.name <- paste("col.", 1:ncol(volcano), sep="");
sample.label <- as.integer(seq(1, length(sample.name), length = 5));
axis3d('y+',at = sample.index1[sample.label], sample.name[sample.label], cex = 0.3);
axis3d('y',at = sample.index1[sample.label], sample.name[sample.label], cex = 0.3)
axis3d('z',pos=c(0, 0, NA))
ppm.label <- as.integer(seq(1, length(ppm.index), length = 10));
axes3d('x', at=c(ppm.index1[ppm.label], 0, 0), abs(round(ppm.index[ppm.label], 2)), cex = 0.3);
title3d(main = title.name, sub = "test", xlab = "ppm", ylab = "samples", zlab = "peak")
rgl.bringtotop();

Monday, October 20, 2008
How to show the distribution of several data set together
# simulate data
x1 <- rnorm(1000, 0.4, 0.8)
x2 <- rnorm(1000, 0.0, 1.0)
x3 <- rnorm(1000, -1.0, 1.0)
# density plots
plot(density(x1), xlim=range( c(x1, x2, x3) ), main="", xlab="" )
lines(density(x2), col=2)
lines(density(x3), col=3)
# rug plots for displaying actual data points
rug(x1, col=1, ticksize=0.01, line=2.5)
rug(x2, col=2, ticksize=0.01, line=3.0)
rug(x3, col=3, ticksize=0.01, line=3.5)

#========================================================
# or use stacking box plot
x1 <- rnorm(1000, 0.4, 0.8)
x2 <- rnorm(1000, 0.0, 1.0)
x3 <- rnorm(1000, -1.0, 1.0)
all <- c(x1, x2, x3);
hist(x1, breaks=seq(min(all), max(all)+0.999, by=0.1),
xlim = c(min(all), max(all+0.01)), ylim=c(0, 55),
main = "hist", xlab = "distribution", ylab= "", col=1);
box();
par(new=T);
hist(x2, breaks=seq(min(all), max(all)+0.999, by=0.1),
xlim = c(min(all), max(all+0.01)), ylim=c(0, 55),
main = "", xlab = "", ylab= "", col=2);
box();
par(new=T);
hist(x3, breaks=seq(min(all), max(all)+0.999, by=0.1),
xlim = c(min(all), max(all+0.01)), ylim=c(0, 55),
main = "", xlab = "", ylab= "", col=3);
box();

x1 <- rnorm(1000, 0.4, 0.8)
x2 <- rnorm(1000, 0.0, 1.0)
x3 <- rnorm(1000, -1.0, 1.0)
# density plots
plot(density(x1), xlim=range( c(x1, x2, x3) ), main="", xlab="" )
lines(density(x2), col=2)
lines(density(x3), col=3)
# rug plots for displaying actual data points
rug(x1, col=1, ticksize=0.01, line=2.5)
rug(x2, col=2, ticksize=0.01, line=3.0)
rug(x3, col=3, ticksize=0.01, line=3.5)

#========================================================
# or use stacking box plot
x1 <- rnorm(1000, 0.4, 0.8)
x2 <- rnorm(1000, 0.0, 1.0)
x3 <- rnorm(1000, -1.0, 1.0)
all <- c(x1, x2, x3);
hist(x1, breaks=seq(min(all), max(all)+0.999, by=0.1),
xlim = c(min(all), max(all+0.01)), ylim=c(0, 55),
main = "hist", xlab = "distribution", ylab= "", col=1);
box();
par(new=T);
hist(x2, breaks=seq(min(all), max(all)+0.999, by=0.1),
xlim = c(min(all), max(all+0.01)), ylim=c(0, 55),
main = "", xlab = "", ylab= "", col=2);
box();
par(new=T);
hist(x3, breaks=seq(min(all), max(all)+0.999, by=0.1),
xlim = c(min(all), max(all+0.01)), ylim=c(0, 55),
main = "", xlab = "", ylab= "", col=3);
box();

Wednesday, October 8, 2008
apply, with and by summary
apply(X, MARGIN, FUN), MARGIN 1 indicates rows, 2 indicates columns
tapply(X, INDEX, FUN) Apply a function to each cell of a factored array
lapply returns a list each element of which is the result of applying FUN to the corresponding list
sapply is a “user-friendly” version of lapply by default returning a vector or matrix if appropriate.
mapply is a multivariate version of sapply applies FUN to the first elements of each ... argument
ex. apply(x, 2, sum), x is a matrix
lapply returns a list of the same length as X, each element of which is the result of applying FUN to the corresponding element of X.
> x <- list(a = 1:10, beta = exp(-3:3), logic = c(TRUE,FALSE,FALSE,TRUE)) >
> x
$a
[1] 1 2 3 4 5 6 7 8 9 10
$beta
[1] 0.04978707 0.13533528 0.36787944 1.00000000 2.71828183 7.38905610 20.08553692
$logic
[1] TRUE FALSE FALSE TRUE
> # compute the list mean for each list element
> lapply(x,mean)
$a
[1] 5.5
$beta
[1] 4.535125
$logic
[1] 0.5
> # median and quartiles for each list element
> lapply(x, quantile, probs = 1:3/4)
$a
25% 50% 75%
3.25 5.50 7.75
$beta
25% 50% 75%
0.2516074 1.0000000 5.0536690
$logic
25% 50% 75%
0.0 0.5 1.0
> sapply(x, quantile)
a beta logic
0% 1.00 0.04978707 0.0
25% 3.25 0.25160736 0.0
50% 5.50 1.00000000 0.5
75% 7.75 5.05366896 1.0
100% 10.00 20.08553692 1.0
sapply is a “user-friendly” version of lapply by default returning a vector or matrix if appropriate.
> mapply(rep, 1:4, 4:1)
[[1]]
[1] 1 1 1 1
[[2]]
[1] 2 2 2
[[3]]
[1] 3 3
[[4]]
[1] 4
> mapply(rep, times=1:4, x=4:1)
[[1]]
[1] 4
[[2]]
[1] 3 3
[[3]]
[1] 2 2 2
[[4]]
[1] 1 1 1 1
tapply(X, INDEX, FUN) Apply a function to each cell of a factored array
> n <- 17; fac <- factor(rep(1:3, len = n), levels = 1:5) > table(fac)
fac
1 2 3 4 5
6 6 5 0
> tapply(1:n, fac, sum)
1 2 3 4 5
51 57 45 NA NA
###################################################
From http://www.statmethods.net/stats/withby.html
With
The with( ) function applys an expression to a dataset. It is similar to DATA= in SAS.
# with(data, expression)
# example applying a t-test to dataframe mydata
with(mydata, t.test(y1,y2))
By
The by( ) function applys a function to each level of a factor or factors. It is similar to BY processing in SAS.
# by(data, factorlist, function)
# example apply a t-test separately for men and women
by(mydata, gender, t.test(y1,y2))
tapply(X, INDEX, FUN) Apply a function to each cell of a factored array
lapply returns a list each element of which is the result of applying FUN to the corresponding list
sapply is a “user-friendly” version of lapply by default returning a vector or matrix if appropriate.
mapply is a multivariate version of sapply applies FUN to the first elements of each ... argument
ex. apply(x, 2, sum), x is a matrix
lapply returns a list of the same length as X, each element of which is the result of applying FUN to the corresponding element of X.
> x <- list(a = 1:10, beta = exp(-3:3), logic = c(TRUE,FALSE,FALSE,TRUE)) >
> x
$a
[1] 1 2 3 4 5 6 7 8 9 10
$beta
[1] 0.04978707 0.13533528 0.36787944 1.00000000 2.71828183 7.38905610 20.08553692
$logic
[1] TRUE FALSE FALSE TRUE
> # compute the list mean for each list element
> lapply(x,mean)
$a
[1] 5.5
$beta
[1] 4.535125
$logic
[1] 0.5
> # median and quartiles for each list element
> lapply(x, quantile, probs = 1:3/4)
$a
25% 50% 75%
3.25 5.50 7.75
$beta
25% 50% 75%
0.2516074 1.0000000 5.0536690
$logic
25% 50% 75%
0.0 0.5 1.0
> sapply(x, quantile)
a beta logic
0% 1.00 0.04978707 0.0
25% 3.25 0.25160736 0.0
50% 5.50 1.00000000 0.5
75% 7.75 5.05366896 1.0
100% 10.00 20.08553692 1.0
sapply is a “user-friendly” version of lapply by default returning a vector or matrix if appropriate.
mapply is a multivariate version of sapply. mapply applies FUN to the first elements of each ... argument> mapply(rep, 1:4, 4:1)
[[1]]
[1] 1 1 1 1
[[2]]
[1] 2 2 2
[[3]]
[1] 3 3
[[4]]
[1] 4
> mapply(rep, times=1:4, x=4:1)
[[1]]
[1] 4
[[2]]
[1] 3 3
[[3]]
[1] 2 2 2
[[4]]
[1] 1 1 1 1
tapply(X, INDEX, FUN) Apply a function to each cell of a factored array
> n <- 17; fac <- factor(rep(1:3, len = n), levels = 1:5) > table(fac)
fac
1 2 3 4 5
6 6 5 0
> tapply(1:n, fac, sum)
1 2 3 4 5
51 57 45 NA NA
###################################################
From http://www.statmethods.net/stats/withby.html
With
The with( ) function applys an expression to a dataset. It is similar to DATA= in SAS.
# with(data, expression)
# example applying a t-test to dataframe mydata
with(mydata, t.test(y1,y2))
By
The by( ) function applys a function to each level of a factor or factors. It is similar to BY processing in SAS.
# by(data, factorlist, function)
# example apply a t-test separately for men and women
by(mydata, gender, t.test(y1,y2))
Subscribe to:
Comments (Atom)
